🎉 FUN WITH CATEGORIES 🎉
Marco Perone

What is category theory?
Category Theory is indeed general abstract nonsense and that it is precisely because of that that it is so important both mathematically and philosophically.








A Category Theory library
- practically usable
- verified

Types allow us to encode proofs
data LTE : (n, m : Nat) -> Type where
LTEZero : LTE Z right
LTESucc : LTE left right -> LTE (S left) (S right)Haskell
head : List A -> ASafer Haskell
headMaybe : List A -> Maybe AIdris
nonEmptyHead : (l : List A ** IsNonEmpty l) -> AWhat is a category?
Objects
Morphisms
Composition
Composition
Composition
Composition
Composition
Composition
Composition
Composition
Identities
Identities
Coherence conditions
Left identity
Left identity
Right identity
Right identity
Associativity
Associativity
Associativity
Associativity
Associativity
Associativity
What is a functor?
Mapping objects
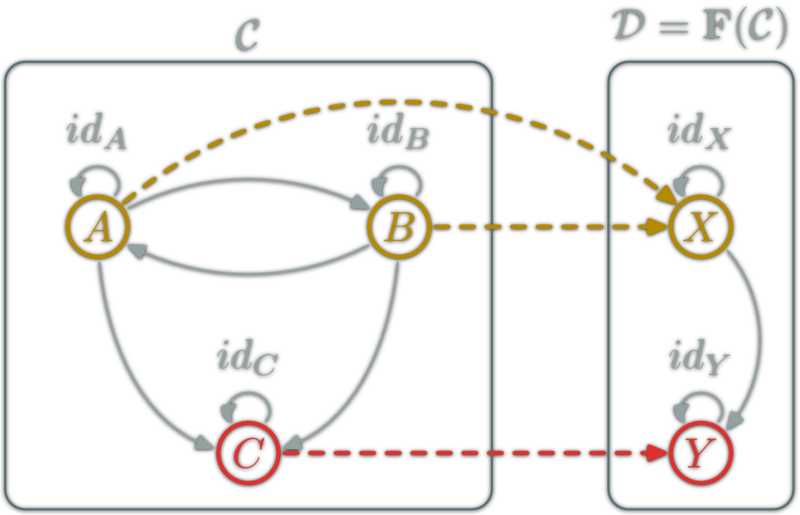
Mapping morphisms
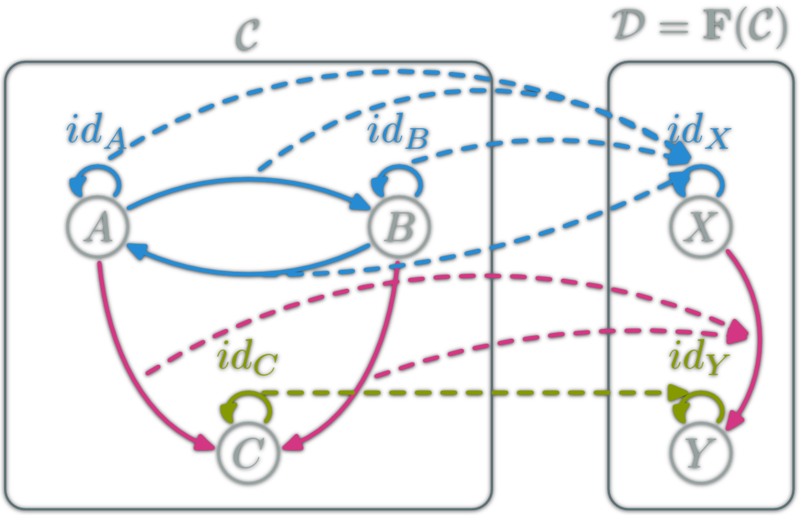
DEMO TIME
Consider a graph
Make a category out of it
Map out of it with a functor
Map out of it with a functor
Map out of it with a functor
Choose a path
Provide initial value
Recap
- Categorise it
- Add a semantic
- 🎉 HAVE FUN 🎉

Resources
🎉 FUN WITH CATEGORIES 🎉